# install.packages("pacman")
library(pacman)
p_load(tidyverse, # データセットのハンドリング
lubridate, # 時間データのハンドリング
causaldata, # データセット集
labelled, # 変数のラベルの調整
ggdag, # DAGを描く
gtsummary, # データの要約
survival, # 生存時間解析
ggsurvfit, # 生存時間解析
WeightIt, # 逆確率重み付け
cobalt, # 標準化差
broom, # 結果の整形
gt # 表の出力
)Part 3: 推測統計の可視化
例:生存時間解析
1 Package
2 Data source
本パートでは、causaldata packageに格納されているNational Health and Nutrition Examination Survey Data I Epidemiologic Follow-up Study (NHEFS)のnhefsデータセットを用います1。観察研究から得られたデータです。このデータセットは、“Causal Inference: What If” by Hernán and Robinsでも具体例として使用されています。
また、前パートでは欠測データの可視化をするために、nhefsデータセットを使いましたが、本パートでは解析をシンプルにするために、欠測データのある症例を取り除いたnhefs_completeデータセットを用います2。
data(nhefs_complete)
var_label(nhefs_complete) <- NULL # nhefs_complete に入っている変数説明情報を削除データセット仕様書は配布しているファイルをご確認ください。R上でも、?nhefs_codebook と入力することでpackageに格納されている仕様を確認できます。
nhefsデータセットは、67変数が1,566例分格納されています。本パートでは説明を簡単にするために、下記の変数のみを扱います。
seqn, death, yrdth, modth, dadth, sex, age, race, education, exercise, smokeintensity, smokeyrs
また、nhefsデータ中のカテゴリカルデータは数値として格納されています。データセット仕様書を見れば内容は把握できるのですが、確認しやすくするためにforcatsパッケージの関数を使ってデータを変換します。
df01 <- nhefs_complete |>
# 変数選択
select(seqn, death, yrdth, modth, dadth, sex, age, race, education, exercise, smokeintensity, smokeyrs) |>
# カテゴリー化、ラベリング
mutate(
sex = factor(sex,
labels = c("Male", "Female")),
race = factor(race,
labels = c("White", "Black or other")),
education = factor(education,
labels = c("8th grade or less",
"HS dropout",
"HS",
"College dropout",
"College or more")),
exercise = factor(exercise,
labels = c("Much exercise",
"Moderate exercise",
"Little or no exercise"))
)3 Question
本パートでは、喫煙の程度が死亡に影響するか評価します。
これは「喫煙の程度が死亡という結果の原因になっているのか」という問いであり、問いの型は因果推論になります。
4 Data
4.1 Outcome
本パートのアウトカム変数は死亡です。ただし、生存・死亡という二値変数だけではなく、観察を開始してからイベント(たとえば死亡)を起こすまでの時間も解析に用います。このようなデータを生存時間データといい、時間とイベントを組み合わせたデータで定義します3。NHEFSの研究では、1983年1月1日がコホートの観察開始日で、1992年12月31日が観察終了日です。これらの情報と
death: 1992年までに死亡したかどうかを示す変数yrdth: 死亡した年modth: 死亡した月dadth: 死亡した日
の情報を組み合わせて、生存時間データを作ります。
df02 <- df01 |>
mutate(
# 死亡日または打ち切り日作成
event_date = if_else(death == 0, ymd("1992-12-31"),
ymd(19000000 + yrdth * 10000 + modth * 100 + dadth)
),
# 観察開始日からの日数を計算
survtime = difftime(time1 = event_date,
time2 = ymd("1983-01-01")
)
)今後、deathとsurvtimeを生存時間データとして扱います。
生存時間データを用いた解析を一般に生存時間解析といいます。
4.2 Exposure
本パートの曝露変数はPack-yearsです。Pack-yearsは喫煙の程度を示す国際的な指標で、次式で定義されます。
df03 <- df02 |>
mutate(
pack_years_n = (smokeintensity / 20) * smokeyrs
)この値は連続尺度データです。(再び)簡単のために、二値変数に変換します。本パートでは20をカットオフ値とします4。Pack-yearsが20以上を高い群、20未満を低い群と定義します。
df04 <- df03 |>
mutate(
pack_years = if_else(pack_years_n >= 20, 1, 0),
pack_years = factor(pack_years,
labels = c("Low", "High"))
)4.3 練習のためのデータ変更
さて、nhefs_completeデータはすべての人が観察期間終了までフォローできているデータです。しかし、実際にみなさんが扱うデータは観察期間終了まで研究対象者をフォローすることは途中で転院等の事象が発生するため困難です。このとき、研究期間中の打ち切りが生じます。このような打ち切りがある場合、後述する生存時間解析で作成する図表には工夫が必要になります。練習のために、研究期間中の打ち切りを発生させたデータセットを作り、今後使用します。
set.seed(1234)
df05 <- df04 |>
mutate(death1 = rbinom(1566, 1, 0.6),
death0 = rbinom(1566, 1, 0.4),
death2 = if_else(pack_years == "High", death1, death0),
censor = rbinom(1566, 1, 0.2),
r_time = if_else(censor == 1 & death == 0 | death2 == 1 & death == 0,
round(runif(1566, min = 0, 3652)), 0),
death = if_else(death2 == 1, 1, death),
survtime = survtime - r_time,
survtime_y = as.numeric(survtime) / 365.25)4.4 本パートで仮定した因果構造
前節で定義した、死亡までの生存時間データ(death, censor, survtime)をアウトカム変数、喫煙の程度(pack_years)を曝露変数とします。喫煙の程度が死亡に影響するか評価するときに、二値化したPack-yearsごとの死亡の発生率を単純に比較することができますが、これでは影響の評価として十分ではありません。Pack-yearsの高い群と低い群で背景情報が異なり、交絡バイアス5が生じる可能性があるからです。
交絡を軽減するためには、交絡を生み出す要因である交絡因子を調整する必要があります。交絡因子は、曝露にもアウトカムにも影響を与える要因です6。変数間の関係、つまり因果構造を頭の中で考えることもできますが、一定のルールのもと可視化するのが便利です。この因果構造を可視化するツールをDAG (Directed Acyclic Graph: 有向非巡回グラフ)といいます。
DAGは、ある変数が別の変数に影響を与えるかどうかを矢印で表します。矢印は常に一方通行です。
紙にざっと書いてしまっても良いのですが、記録として残しやすくするためにRで描いてみましょう。データセットの中で交絡因子になり得る変数は、sex, age, race, education, exercise です。これらが、deathとpack_yearsにどのように影響するか可視化してみましょう。描画はggdagパッケージを用います7。
dag01 <- dagify(
# 因果構造の指定
death ~ pack_years + sex + age + race + education + exercise,
pack_years ~ sex + age + race + education + exercise,
exposure = "pack_years",
outcome = "death",
# 変数の位置指定
coords = list(
x = c(pack_years = 0,
sex = 1,
age = 1.5,
race = 3,
education = 4.5,
exercise = 5,
death = 6),
y = c(pack_years = 0,
sex = 1.5,
age = 1,
race = 1.5,
education = 1,
exercise = 1.5,
death = 0)
),
# 変数のラベリング
labels = c(
"pack_years" = "Pack years",
"sex" = "Sex",
"age" = "Age",
"race" = "Race",
"education" = "Education",
"exercise" = "Exercise",
"death" = "Death")
) |>
tidy_dagitty()
ggdag(dag01,
text = FALSE,
use_labels = "label") +
theme_dag()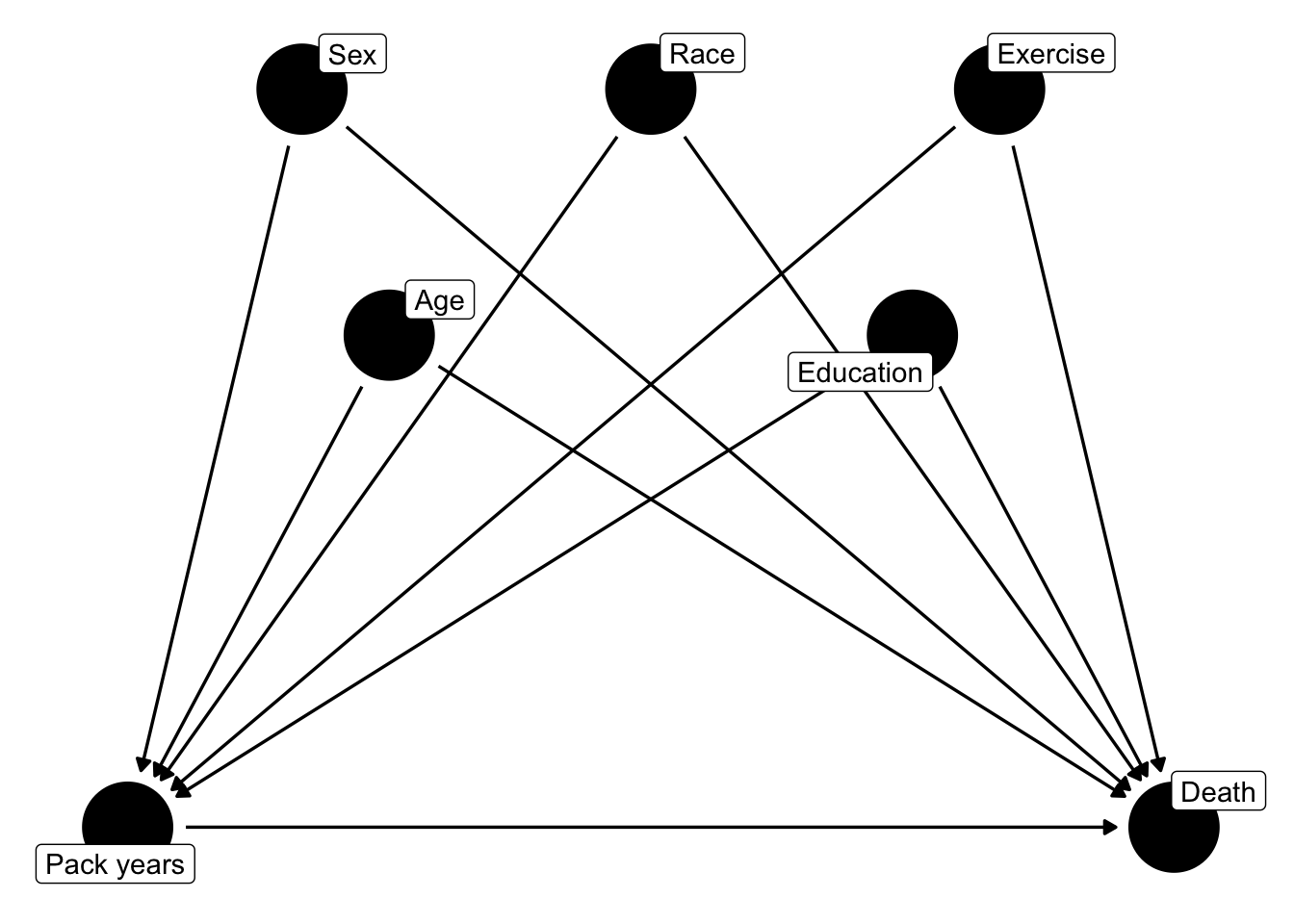
描画したDAGの通り、交絡バイアスを引き起こす候補因子はすべて曝露にもアウトカムにも影響を与えます。そのため、これらの変数はすべて交絡因子と考えられます。
またggdagパッケージには、よりフォーマルな交絡因子の選択基準であるバックドア基準を用いて、交絡因子を同定する関数があります。鮭の切り身の色の変数が交絡因子となる変数です。交絡因子は、Pack-yearsのDeathへの影響評価時に調整する必要があるため、adjustedと表記されています。
ggdag_adjustment_set(dag01,
text = FALSE,
use_labels = "label",
shadow = TRUE) +
theme_dag()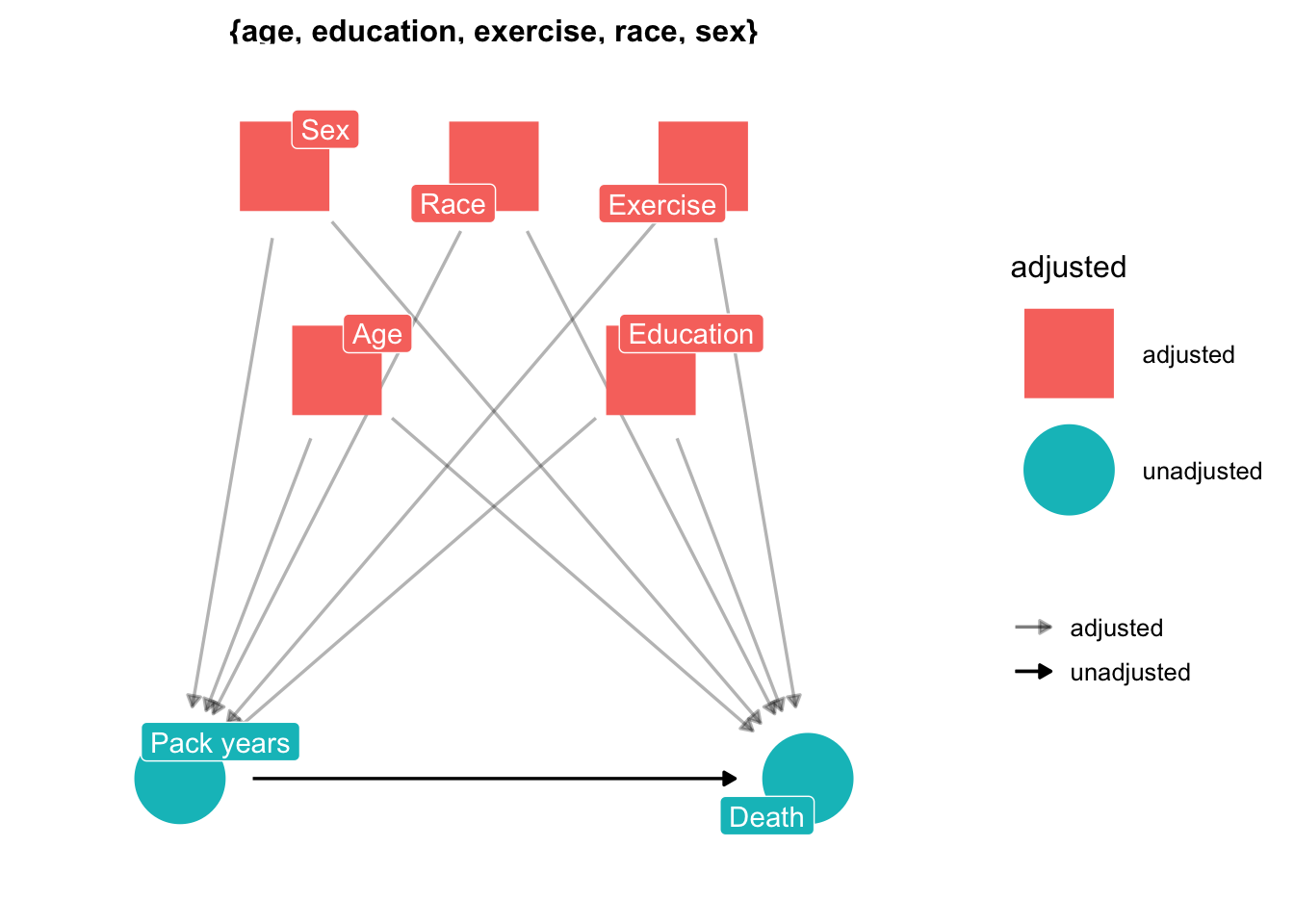
5 統計解析
5.1 背景情報の要約
研究対象集団の情報(特徴)を要約することは重要です。この情報をもとに、研究者は自分がもともと想定していた集団であるか、読者は目の前の患者さん等に研究の結果を適用できるか検討できます。本パートでは、Pack-yearsの区分ごとにsex, age, race, education, exercise の情報を要約します。論文ではTable 1として載せることが多いです8。
背景情報の要約は、gtsummaryパッケージを使うと容易におこなえます。結果より、すべての変数において要約統計量が群間で異なり、群間で背景情報がずれていることがわかります。つまり、単純に解析すると、背景情報が異なることにより交絡バイアスが生じ、喫煙の程度と死亡との関連を推定しても、推定値を効果と解釈することはできません。
では、gtsummaryを使ってTable 1を作っていきます。まず最も簡単な設定だとこうなります。
df05 |>
select(pack_years, # 曝露変数
sex, age, race, education, exercise # 背景情報
) |>
tbl_summary()| Characteristic | N = 1,5661 |
|---|---|
| pack_years | |
| Low | 744 (48%) |
| High | 822 (52%) |
| sex | |
| Male | 762 (49%) |
| Female | 804 (51%) |
| age | 43 (33, 53) |
| race | |
| White | 1,360 (87%) |
| Black or other | 206 (13%) |
| education | |
| 8th grade or less | 291 (19%) |
| HS dropout | 340 (22%) |
| HS | 637 (41%) |
| College dropout | 121 (7.7%) |
| College or more | 177 (11%) |
| exercise | |
| Much exercise | 300 (19%) |
| Moderate exercise | 661 (42%) |
| Little or no exercise | 605 (39%) |
| 1 n (%); Median (IQR) | |
これだけですとTable 1と不十分です。上の表をベースに情報を付け足していきます。要領はggplotと同じです。では、次の情報を付け足して、下の表を作りましょう。公式ページの情報も参考になります。
群ごとに要約する(tbl_summary関数の
by引数を使う)群間比較のP値を算出する(
add_p()を追加する)
Code
df05 |>
select(pack_years, # 曝露変数
sex, age, race, education, exercise # 背景情報
) |>
tbl_summary(by = pack_years) |> # 群間比較にする
add_p()| Characteristic | Low, N = 7441 | High, N = 8221 | p-value2 |
|---|---|---|---|
| sex | <0.001 | ||
| Male | 282 (38%) | 480 (58%) | |
| Female | 462 (62%) | 342 (42%) | |
| age | 34 (29, 46) | 48 (42, 56) | <0.001 |
| race | <0.001 | ||
| White | 602 (81%) | 758 (92%) | |
| Black or other | 142 (19%) | 64 (7.8%) | |
| education | <0.001 | ||
| 8th grade or less | 105 (14%) | 186 (23%) | |
| HS dropout | 133 (18%) | 207 (25%) | |
| HS | 331 (44%) | 306 (37%) | |
| College dropout | 70 (9.4%) | 51 (6.2%) | |
| College or more | 105 (14%) | 72 (8.8%) | |
| exercise | 0.075 | ||
| Much exercise | 160 (22%) | 140 (17%) | |
| Moderate exercise | 308 (41%) | 353 (43%) | |
| Little or no exercise | 276 (37%) | 329 (40%) | |
| 1 n (%); Median (IQR) | |||
| 2 Pearson's Chi-squared test; Wilcoxon rank sum test | |||
gtsummary packageはもっと細かい設定もできます。
5.2 アウトカムの分布の確認
アウトカムである死亡までの時間が群間でどのように分布するか要約します。生存時間データの場合、Kaplan-Meier曲線を使って時間の経過にともなう生存確率の変化を可視化します9。
最も簡単な設定だとこうなります。
# Kaplan-Meier推定
# Kaplan-Meier方に基づく生存確率を推定
km_simple <- survfit2(Surv(survtime_y, death) ~ pack_years, data = df05)
ggsurvfit(km_simple)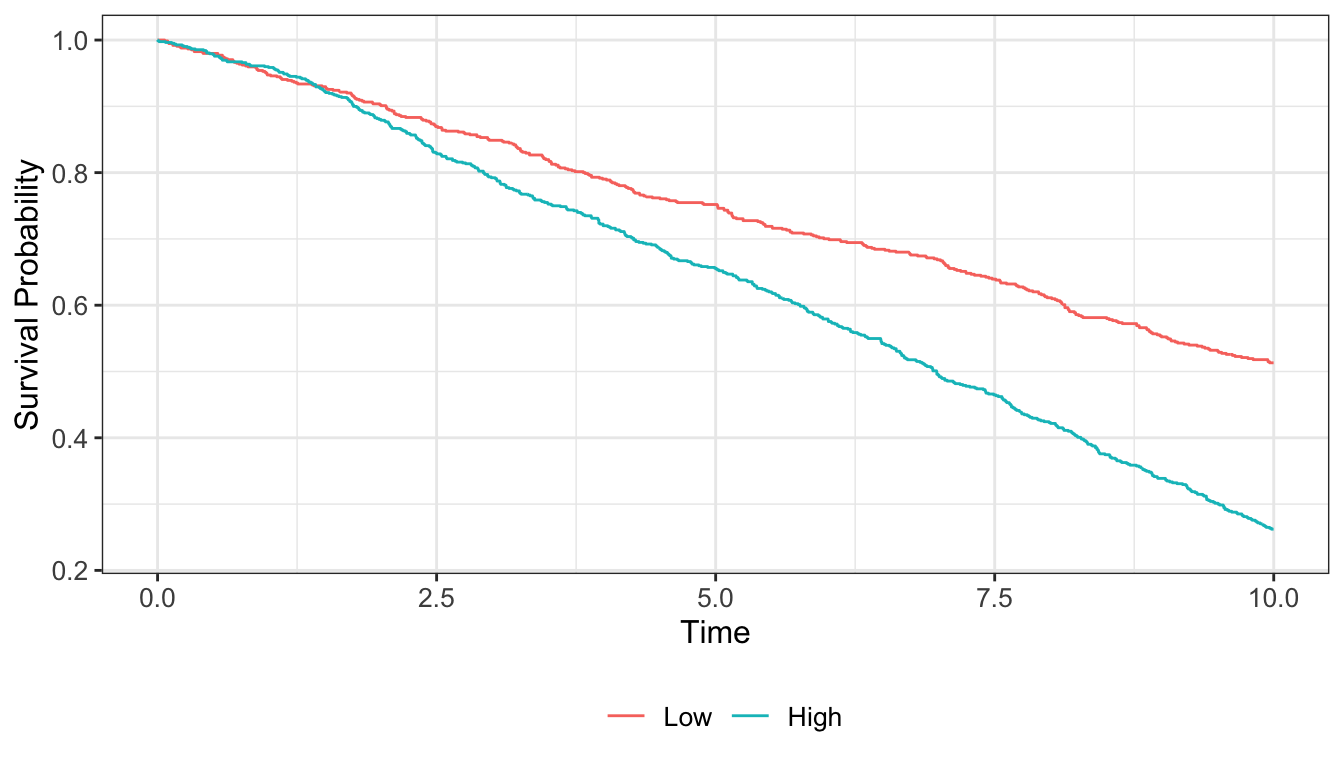
これでも群ごとの生存確率の推移はわかります。しかしKaplan-Meier曲線は論文中にも載せることも多く、細かいところに気を配りながら図を作成する方が良いです。
たとえば、Y軸は確率なので、0から1の範囲であることを明確に示す方が好まれます。
ggsurvfit(km_simple) +
scale_y_continuous(limits = c(0, 1),
breaks = seq(0, 1, by = 0.2))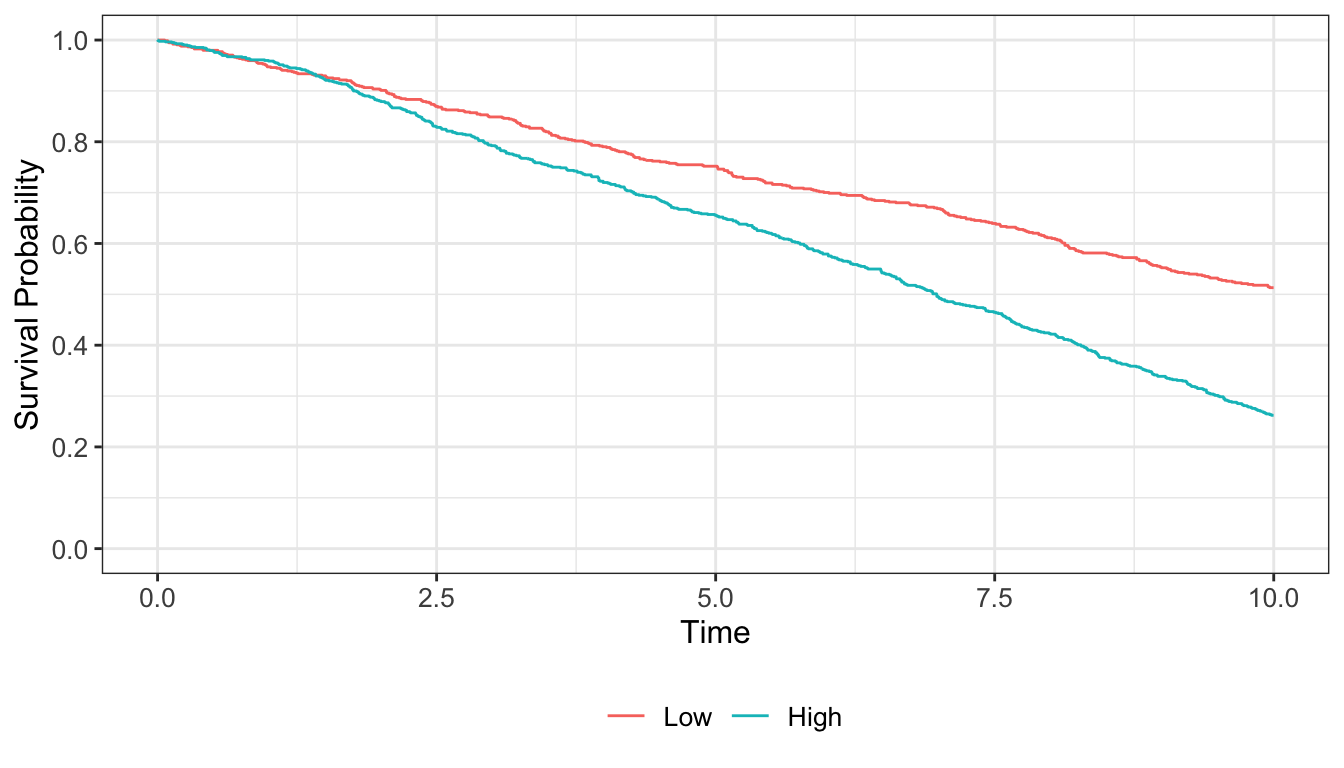
さらに次の情報を足して、魅力的な生存時間分布の図を作成しましょう。これも要領はggplotと同じです。
X軸とY軸に任意のタイトルをいれる(
labs(x = "Years", y = "Overall survival probability")を追加する)Kaplan-Meier曲線に95%信頼区間をつける(
add_confidence_interval()を追加する)打ち切り(ひげ)をつける(
add_censor_mark()を追加する)No at risk表をつける(
add_risktable(risktable_stats = c("n.risk", "cum.event", "cum.censor"))を追加する)生存時間中央値を示す(
add_quantile()を追加する)X軸の目盛りをわかりやすくする(
scale_x_continuous(limits = c(0, 10), breaks = seq(0, 10, by = 1))を追加する)
Code
# Kaplan-Meier曲線の描画
ggsurvfit(km_simple) +
scale_y_continuous(limits = c(0, 1),
breaks = seq(0, 1, by = 0.2)) +
labs(
x = "Years",
y = "Overall survival probability"
) +
add_confidence_interval() + # 信頼区間をつける
add_censor_mark() + # 打ち切りをつける
# No at risk表をつける
add_risktable(risktable_stats = c("n.risk", "cum.event", "cum.censor")) +
add_quantile() + # 生存時間中央値を示す
scale_x_continuous(limits = c(0, 10),
breaks = seq(0, 10, by = 1))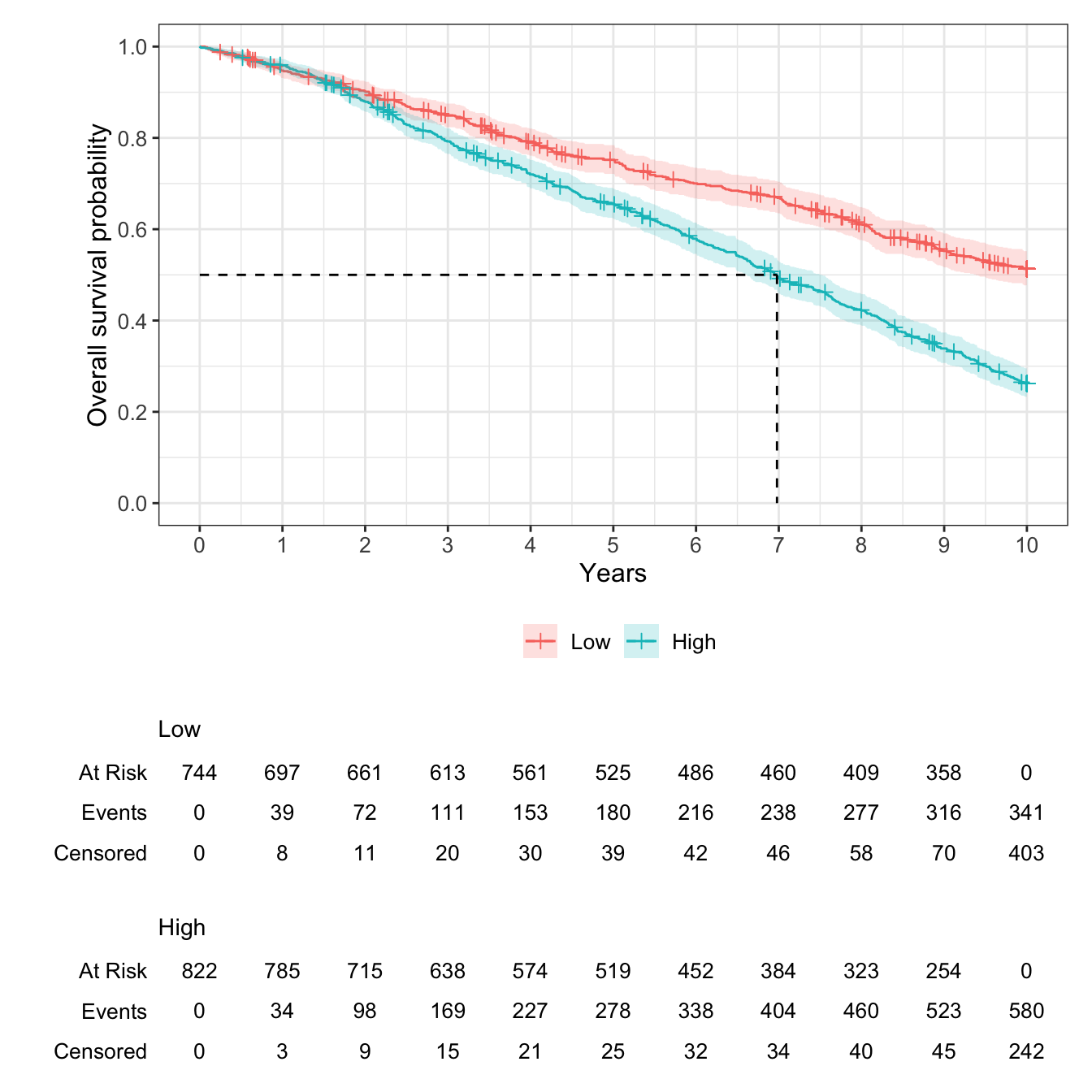
この図より、喫煙量が多い集団の方が低い集団に比べて、生存確率が全体的に低いことが見てとれます。
5.3 喫煙の程度と死亡との関連評価
次に単純な推定により、曝露とアウトカムとの関連を評価します。
5.3.1 生存時間中央値(MST: Median Survival Time)
生存時間中央値は生存確率が50%になる時点のことです。
km_simpleCall: survfit(formula = Surv(survtime_y, death) ~ pack_years, data = df05)
n events median 0.95LCL 0.95UCL
pack_years=Low 744 341 NA 9.38 NA
pack_years=High 822 580 6.98 6.62 7.51medianが生存時間中央値であり、0.95LCLと0.95UCLは95%信頼区間を示します。
5.3.2 群の時点ごとの生存確率と95%信頼区間
群ごと時点ごとの生存確率を推定します。times引数により任意の時点における生存確率を推定することができます。
summary(km_simple, times = seq(0,10, by =1))Call: survfit(formula = Surv(survtime_y, death) ~ pack_years, data = df05)
pack_years=Low
time n.risk n.event survival std.err lower 95% CI upper 95% CI
0 744 0 1.000 0.00000 1.000 1.000
1 697 39 0.947 0.00822 0.931 0.964
2 661 33 0.902 0.01093 0.881 0.924
3 613 39 0.849 0.01323 0.823 0.875
4 561 42 0.790 0.01509 0.761 0.820
5 525 27 0.752 0.01606 0.721 0.784
6 486 36 0.700 0.01711 0.667 0.735
7 460 22 0.668 0.01762 0.635 0.704
8 409 39 0.611 0.01834 0.576 0.648
9 358 39 0.552 0.01885 0.516 0.590
pack_years=High
time n.risk n.event survival std.err lower 95% CI upper 95% CI
0 822 0 1.000 0.00000 1.000 1.000
1 785 34 0.959 0.00695 0.945 0.972
2 715 64 0.880 0.01136 0.858 0.903
3 638 71 0.792 0.01423 0.765 0.821
4 574 58 0.720 0.01579 0.690 0.751
5 519 51 0.656 0.01674 0.624 0.689
6 452 60 0.579 0.01746 0.546 0.614
7 384 66 0.495 0.01775 0.461 0.531
8 323 56 0.422 0.01761 0.389 0.458
9 254 63 0.339 0.01696 0.307 0.374timeが時点、survivalが生存確率、lower 95% CIとupper 95% CIが95%信頼区間です。
5.3.3 生存確率の群間比較
群間の生存確率が異なるかどうかは、Logrank検定で推定できます。有意水準は5%とします。
survdiff(Surv(survtime_y, death) ~ pack_years, data = df05)Call:
survdiff(formula = Surv(survtime_y, death) ~ pack_years, data = df05)
N Observed Expected (O-E)^2/E (O-E)^2/V
pack_years=Low 744 341 477 38.9 81.4
pack_years=High 822 580 444 41.9 81.4
Chisq= 81.4 on 1 degrees of freedom, p= <2e-16 P値が有意水準未満であることから、喫煙の程度と死亡との間には関連が認められることがわかります。
このようにKaplan-Meier曲線で生存確率を可視化したり、単純な解析で傾向を把握することは、思わぬミス(群のコーディングを逆にしていた。生存と死亡が逆だった等)を防いだり、その後の解析から得られる結果の洞察を深めるためにも重要です。
ここまでの解析で喫煙の程度と死亡には関連が認められることがわかりましたが、これから喫煙の程度が死亡に影響するか評価していきます。
5.4 喫煙の程度の死亡への影響評価
ここから、喫煙の程度が死亡に影響するか評価していきます。ポイントはバイアス、特に交絡バイアスの軽減です。バイアスを調整する方法は大きく2つに分かれます。
- アウトカムモデル:アウトカムに対する回帰
- PSモデル:曝露に対する回帰
1はCox比例ハザードモデルの説明変数に曝露変数と交絡因子を入れたモデルにより、アウトカムに対する曝露の影響を評価します。アウトカムに対して直接モデルを構築するため「アウトカムモデル」といいます。
2はまず傾向スコア(PS: Propensity score)を推定し、その後傾向スコアを利用して群間のバランスを調整し、アウトカムに対する曝露の影響を評価します。傾向スコアは個人の背景情報から推定される曝露する確率です。傾向スコアを推定するために曝露に対してモデルを構築するため「PSモデル」といいます。本パートでは、PSモデルを用いて解析を進めます。
バイアスを調整することができれば、喫煙の程度と死亡との間の関連(association)を定量化した推定値(本パートではハザード比10)は、効果(effect)と見なすことができます。
5.4.1 推定目標(Estimand)
まず傾向スコアを算出し、それを利用して群間のバランスをとることでバイアスを調整します。傾向スコアを利用した解析方法はいくつかあり、どの方法でもバイアスを調整することはできます。しかし研究で知りたい効果、つまり推定目標(Estimand)が異なります。
推定目標の代表は、ATEとATTです。
ATEは平均処置効果(Average Treatment Effect)です。これは研究対象集団が仮に全員曝露した場合と、仮に全員曝露しなかった場合のアウトカムの平均値、リスクや率を比較します。今回のテーマでは研究対象集団全員が喫煙量を減らすと予後はどうなるのか、ということに関心があるので推定目標はATEになります。
ATTは処置群における平均処置効果(ATE in the Treatment group)です。ATMはマッチングした集団における平均処置効果(ATE in the matched population)です。Conditional effectは条件付き効果といい、 PSや層が同じ集団におけるATEです。これらの説明は割愛します。
下表に傾向スコアの利用方法と推定目標をまとめました。
| 傾向スコアを利用した解析方法 | 推定目標 |
|---|---|
| 層別解析 | ATE(層を併合)、Conditional effect(層ごと) |
| 回帰 | Conditional effect |
| マッチング | ATT、ATM |
| 逆確率重み付け | ATE |
本テーマの推定目標はATEなので、逆確率重み付けを用いて解析を進めていきます。
5.4.2 逆確率重み付けを用いた群間バランスの調整
逆確率重み付け法(IPW or IPTW: Inverse Probability Treatment Weighting)は、個人ごとに推定した傾向スコアの逆数により、群間のバランスを調整する方法です。詳細な説明は割愛します11。
傾向スコアとその逆確率を計算する方法は複数ありますが、ここではWeightIt packageを使った方法を紹介します。
# 傾向スコアモデルを作り、傾向スコアを推定、ATEを算出するための重み計算まで一気におこなう関数
ipw_model <- weightit(pack_years ~ sex + age + race + education + exercise,
data = df05,
method = "ps",
estimand = "ATE")傾向スコアの分布を確認します。
# バランスの確認
bal.plot(ipw_model,
var.name = "prop.score",
which = "unadjusted",
type = "histogram",
mirror = TRUE)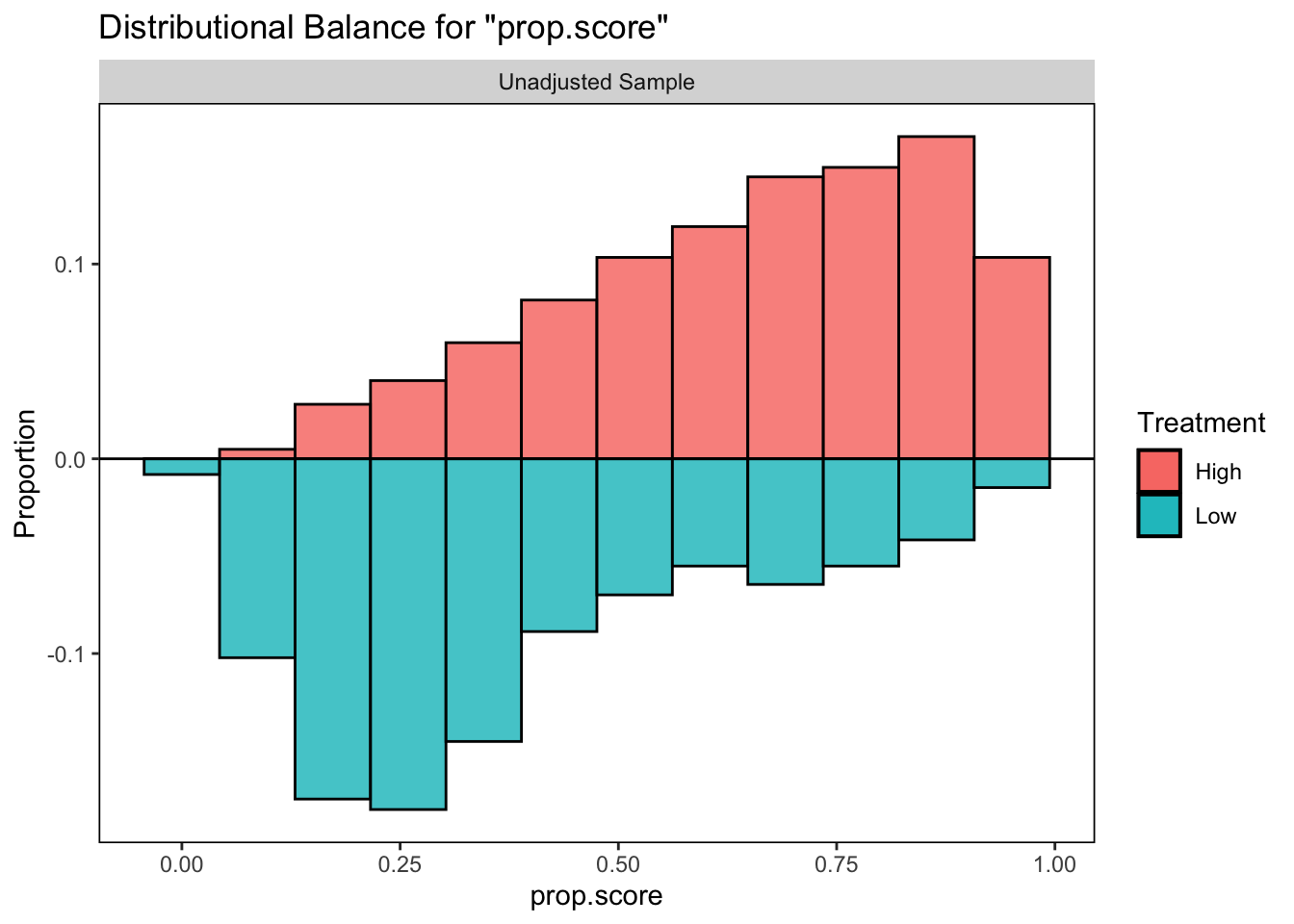
pack_yearsが高い群の方が、背景情報から計算される傾向スコアが全体的に大きいことがわかります。低い群はその逆です。傾向スコアの分布が群間で似ていないため、背景情報のバランスがとれてないことが示唆されます。
ここまで見てきたのは「調整前」の結果です。ここから逆確率重み付けで調整した「調整後」の結果を見ていきます。
まず、調整後の傾向スコアの分布を確認します。which引数を"both"とすれば良いです12。
# バランスの確認
bal.plot(ipw_model,
var.name = "prop.score",
which = "both",
type = "histogram",
mirror = TRUE)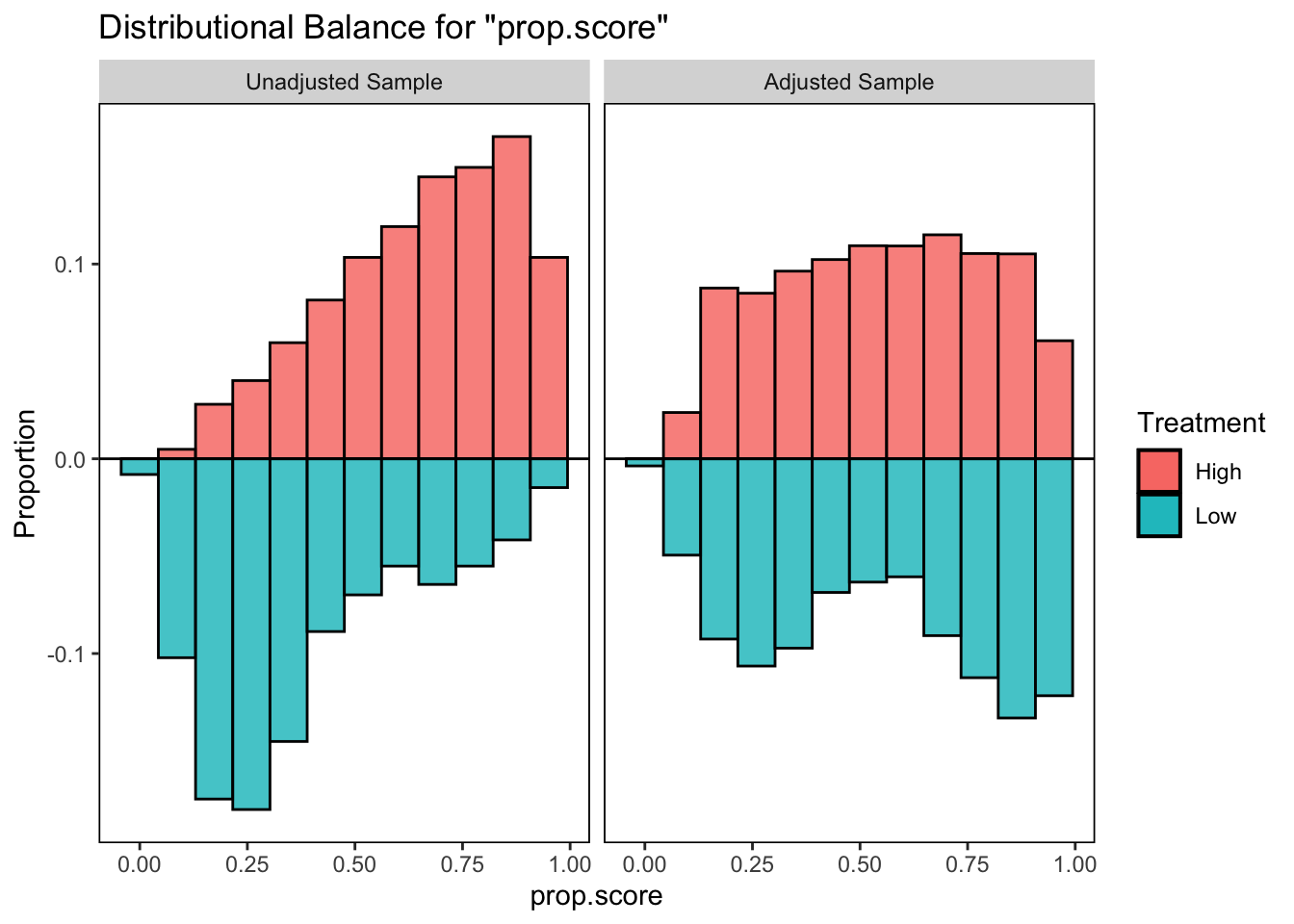
左側が調整前、右側が調整後です。傾向スコアの分布が調整前よりは似通っています。
さらに逆確率重み付け法では、重みの大きさを確認することも重要です。
summary(ipw_model) Summary of weights
- Weight ranges:
Min Max
Low 1.0356 |---------------------------| 44.4839
High 1.0150 |----| 11.1897
- Units with 5 most extreme weights by group:
76 177 641 1037 679
Low 16.9299 21.5032 21.7257 30.6102 44.4839
1497 67 1199 103 1187
High 7.1414 8.0117 8.1201 8.2414 11.1897
- Weight statistics:
Coef of Var MAD Entropy # Zeros
Low 1.211 0.575 0.329 0
High 0.592 0.374 0.127 0
- Effective Sample Sizes:
Low High
Unweighted 744. 822.
Weighted 301.94 608.74最も大きい重みは、pack_years低い群の44.48です。この値程度では問題ないのですが、極端に大きな値の場合注意が必要です13。
次に交絡因子ごとに群間のバランスをlove.plot関数で確認します14。従来は群間のP値で確認していましたが、最近は標準化差(Standardized differences)で確認することが多いです。標準化差の絶対値が0.1以下のときに、その変数は群間でバランスがとれていると経験的に考えます。
まず標準化差を数値として確認します。
bal.tab(ipw_model, un = TRUE)Balance Measures
Type Diff.Un Diff.Adj
prop.score Distance 1.2336 -0.0570
sex_Female Binary -0.2049 0.0089
age Contin. 0.9647 -0.1208
race_Black or other Binary -0.1130 0.0037
education_8th grade or less Binary 0.0851 -0.0194
education_HS dropout Binary 0.0731 0.0153
education_HS Binary -0.0726 0.0105
education_College dropout Binary -0.0320 0.0002
education_College or more Binary -0.0535 -0.0067
exercise_Much exercise Binary -0.0447 0.0055
exercise_Moderate exercise Binary 0.0155 -0.0054
exercise_Little or no exercise Binary 0.0293 -0.0001
Effective sample sizes
Low High
Unadjusted 744. 822.
Adjusted 301.94 608.74数値だとわかりづらいので、可視化します。
love.plot(ipw_model,
thresholds = 0.1,
stars = "raw")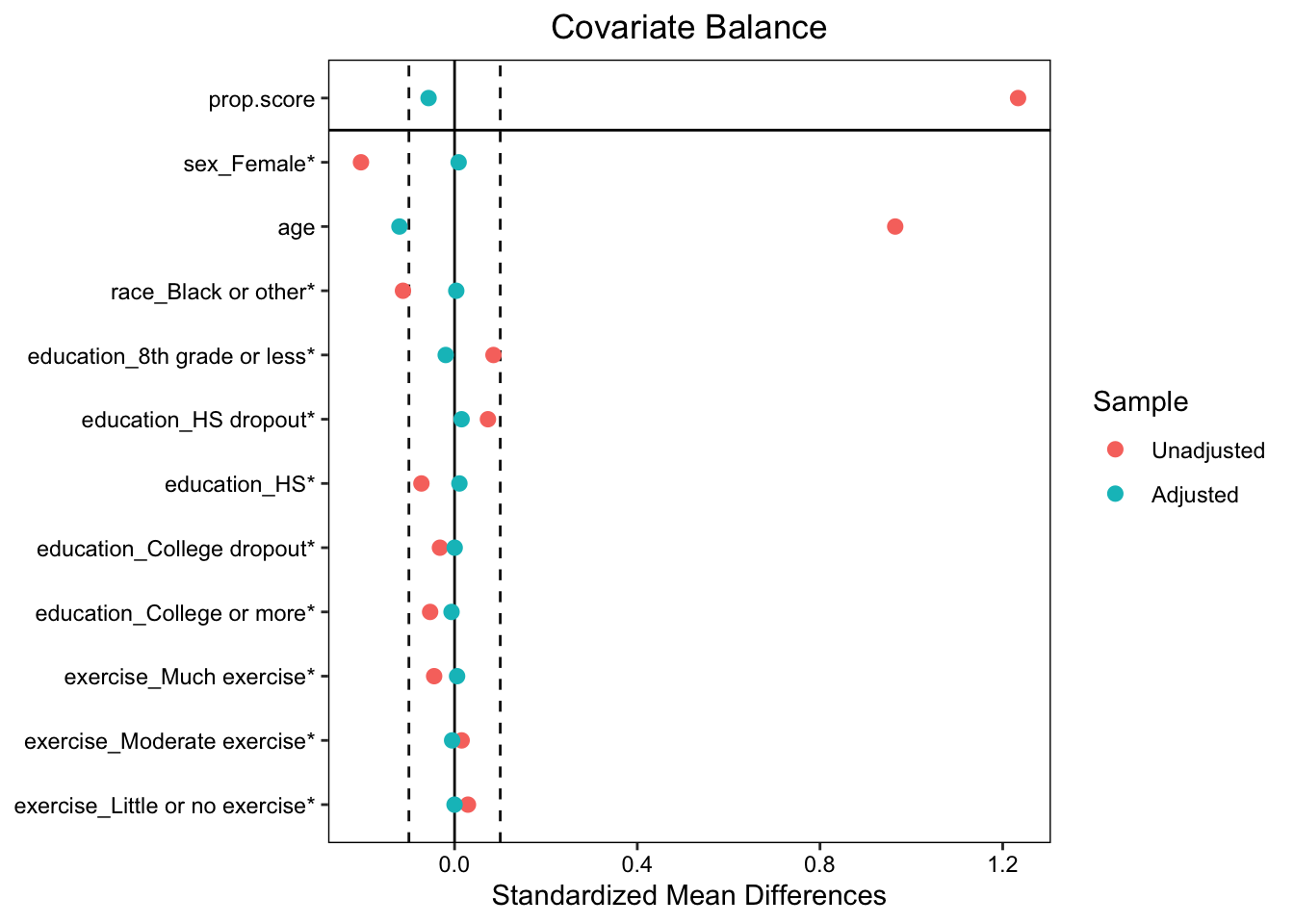
図より、調整後は概ねバランスとれているが、ageとsexが標準化差が0.1より大きいことがわかります。本来ならば、すべてのバランスをとれるように交絡因子を検討し直したり、PSモデルに交互作用や高次の項を含めたり試行錯誤15をおこなった後にATEの推定をおこないますが、今回は練習なので次に進みます。
5.4.3 推定
いよいよATEの推定です。coxph関数に先に推定した重みを指定します。また逆確率重み付け法では交絡を調整するために対象集団を擬似的に膨らましているため、通常の推定では95%信頼区間が過剰に狭くなります。そのためcluster引数で識別変数seqnを指定し、保守的な推定をおこないます。
# 逆確率重み付け法で算出した重みを用いたCox比例ハザードモデル
cox_model_ipw <- coxph(Surv(survtime_y, death) ~ pack_years,
weights = ipw_model$weights,
cluster = seqn,
data = df05
)
# 表の作成
tab_cox_model_ipw <- tidy(cox_model_ipw, conf.int = TRUE, exponentiate = TRUE) %>%
select(term, estimate, conf.low, conf.high, p.value)
# 表の出力
tab_cox_model_ipw |> gt()| term | estimate | conf.low | conf.high | p.value |
|---|---|---|---|---|
| pack_yearsHigh | 1.464304 | 1.232741 | 1.739365 | 1.409734e-05 |
推定した結果、喫煙量が低い群に比べて高い群のハザード比は1.46(95%信頼区間, 1.23 to 1.74, P < 0.001)であり、交絡を調整しても喫煙の程度と死亡には正の関連が認められることがわかります。交絡が十分に調整できていると考えるならば、「喫煙の程度は死亡に影響する」と解釈できます。
最後に、逆確率重み付け法で交絡を調整した生存確率を可視化します。
# 調整した生存確率を推定するためのデータセット作成
df06 <- df05 |>
select(survtime_y, death, pack_years)
# 調整した生存確率を推定
estimated_survival <- predict(cox_model_ipw, df06, type = "survival", se.fit = TRUE)
# 生存確率を可視化するための準備
df07 <- bind_cols(df06,
estimated_survival = estimated_survival$fit,
ucl = estimated_survival$fit + 1.96 * estimated_survival$se.fit,
lcl = estimated_survival$fit - 1.96 * estimated_survival$se.fit)
# 可視化
ggplot(df07, aes(x=survtime_y, y=estimated_survival,
color = pack_years, fill = pack_years)) +
geom_line() +
geom_ribbon(aes(ymin = lcl, ymax = ucl), alpha = 0.3, color = NA) +
xlab("Years") +
ylab("Estimated survival probability from IPW") +
scale_y_continuous(limits = c(0, 1),
breaks = seq(0, 1, by = 0.2)) +
scale_x_continuous(limits = c(0, 10),
breaks = seq(0, 10, by = 1)) +
theme_bw() +
theme(legend.position="bottom")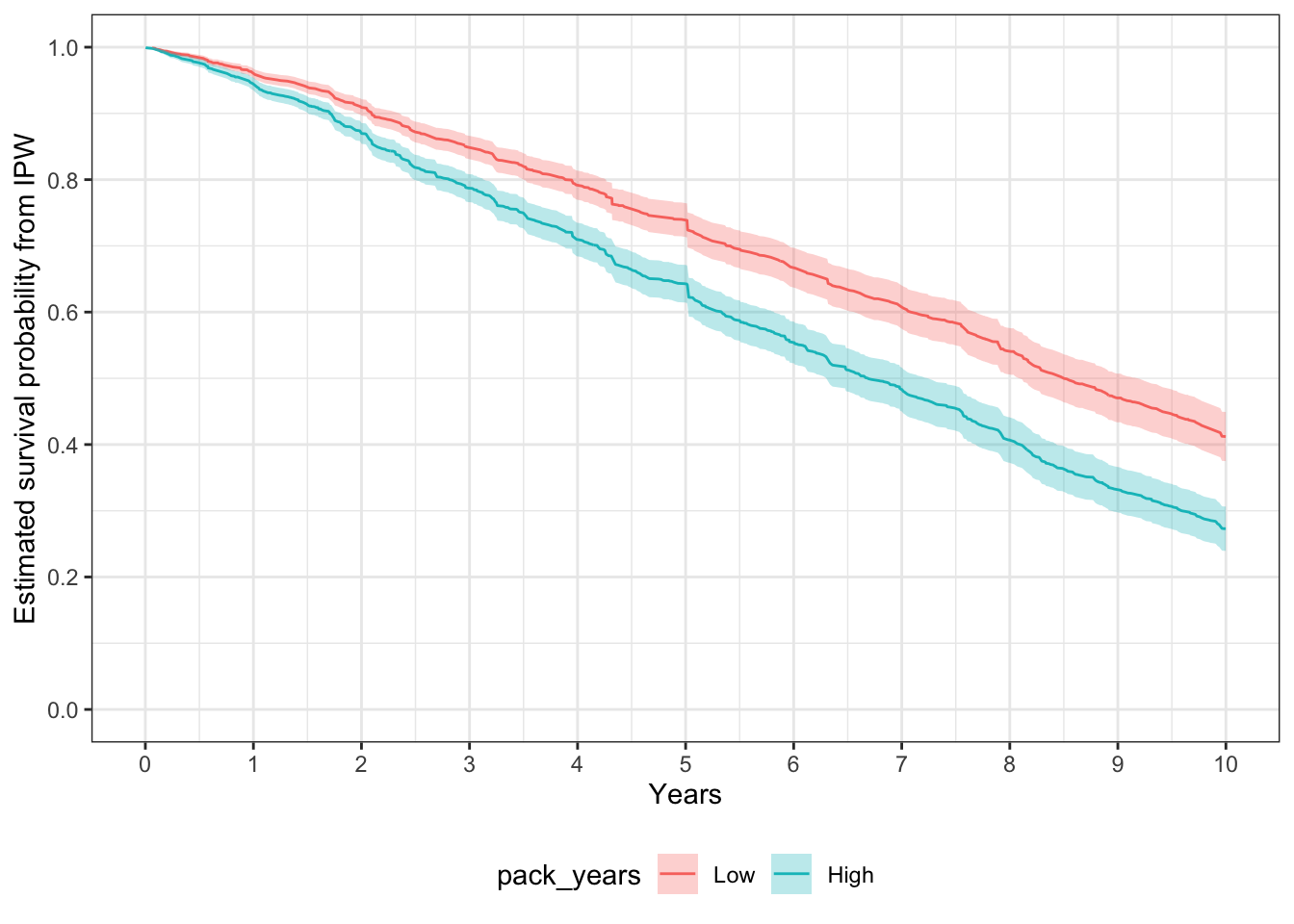
調整前のKaplan-Meier曲線と形状はほぼ同じですが、全体的に生存確率が低くなっていることがわかります。
6 まとめ
生存時間解析の流れを通して、可視化がどのように使われるか見てきました。可視化しなくても推定や検定はおこなえます。しかし可視化することで、思わぬミスを防いだり、よりわかりやすく結果を伝えることができます。
これからも魅力ある可視化をしていきましょう!
Footnotes
データの詳細は、Consoleに
?nhefsと入力してご確認ください。↩︎このように欠測データのある症例を単純に取り除くと選択バイアスが生じるため、実際は多重代入法等の欠測に対する処理をおこないます。↩︎
今回のデータは生存・死亡を扱うため生存時間データという用語に違和感はないですが、退院や製品の故障といったデータも生存時間として解析できます。より広範な用語として、time-to-eventデータというものがあります。↩︎
『COPD(慢性閉塞性肺疾患)診断と治療のためのガイドライン2022(第6版)』よりカットオフ値を引用しました。本来は、自身のCQや関連研究にあわせてカットオフ値を決めてください。中央値や平均値を使うこともできますが、査読時に根拠を求められる可能性が高いです。↩︎
交絡バイアスとは、本来知りたい影響の程度と解析で得られた推定値がずれることをいいます。↩︎
かなり単純な説明にしています。↩︎
パッケージの詳細は次のリンクをご確認ください。https://ggdag.malco.io/index.html↩︎
この表の通称もTable 1です。↩︎
これから使う生存時間解析の手法の詳細については割愛します。『生存時間解析』(杉本知之、朝倉書店)等をご確認ください。↩︎
リスク差、リスク比、オッズ比、率比、平均値の差も定量化した推定値になります↩︎
『統計的因果推論の理論と実装 (Wonderful R)』(高橋将宜、共立出版)等をご確認ください↩︎
流れを理解できているならば、はじめから
which = "both"としても問題ないです。↩︎この場合、重みの両端を取り除く(トリム)方法を使うこともあります。↩︎
細かいですが、標準化差を計算できるのは連続データです。カテゴリカルデータは標準偏差がないために標準化差ではなく、割合の差を計算しています。引数
startsを"raw"にすると、標準化差を出力していないカテゴリカルデータに対してアスタリスク(*)がつきます。↩︎次のステップの推定の前に、群間のバランスがとれて交絡が十分に調整できているか確認できるのが、傾向スコアを用いた解析の良いところです。↩︎